数学新视野：从牛顿-莱布尼兹公式推导出泰勒级数
数学新视野：从牛顿-莱布尼兹公式推导出泰勒级数
泰勒级数是关于函数在某个点的的级数展开。一维泰勒级数是关于一个点 的实函数的展开，由f(x)=a我们得到
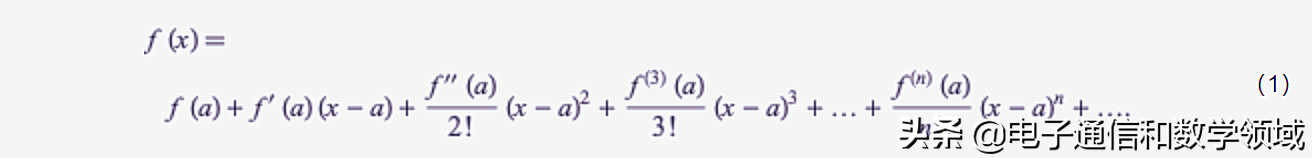
如果a = 0，则扩展为著名的Maclaurin级数。
泰勒定理（实际上是格雷戈里首先发现的）指出，满足某些条件的任何函数都可以表示为泰勒级数
常见的一些泰勒级数包括
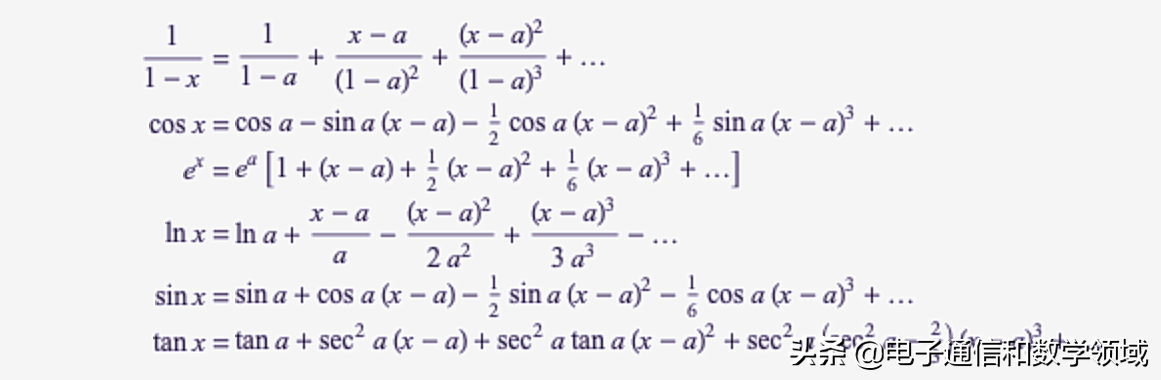
为了推导函数f(x)的泰勒级数，请注意f(x)的(n+1)导数f(n+1)从点x0到任意点x的积分为
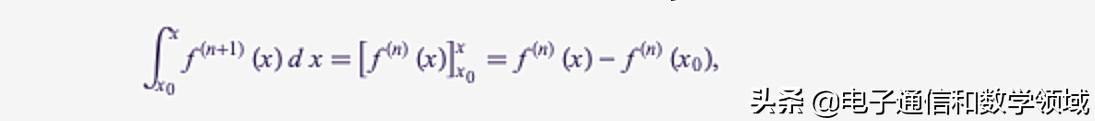
其中f^(n) (x0)是f(x)在x0处的n阶导数，因此它是一个常数。现在第二次积分得到
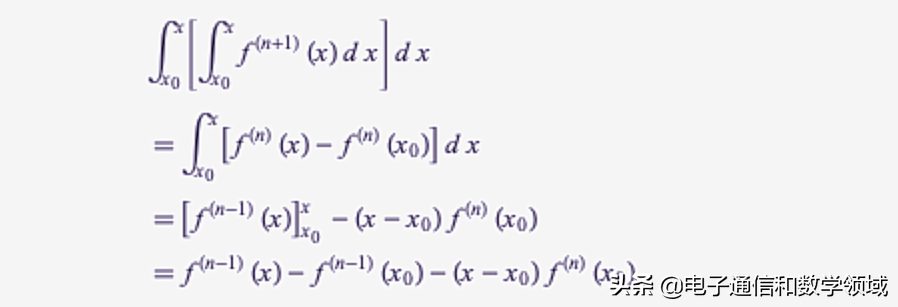
f^(k) (x0)也是一个常数。第三次积分，
一直到n+1个积分，然后得到
重新排列，然后得到一维泰勒级数
这里，Rn是一个余数项,称为拉格朗日余项，由
重写重积分，然后给出
现在，根据函数g(x)的中值定理，
对于[x0,x]中的某个x*。因此，对n+1次积分就得到了结果
-
- 闽南传统民俗拜天公
-
2023-12-15 14:07:47
-
- 联通新出流量卡套餐解析
-
2023-12-15 14:05:32
-
- 李纯否认与李易峰恋情，发飙怒怼网友：满嘴喷粪的畜生！
-
2023-12-15 14:03:17
-
- 抗日战场上 新兵的死亡率总是很高 这点你肯定不知道
-
2023-12-15 14:01:02
-
- 国服第一剑姬和国服第一锐雯究竟谁更强？可乐猛比solo见分晓
-
2023-12-15 13:58:47
-
- 东帝汶是唯一没有加入东南亚联盟的东南亚国家，全国无省，直管县
-
2023-12-15 13:56:32
-
- 带你了解国内有哪些土地性质
-
2023-12-15 13:54:17
-
- 鹿晗晒童年帅照 鹿晗家庭背景揭秘
-
2023-12-15 07:22:10
-
- 连续五年第一！长沙望城长郡月亮岛学校教育质量究竟怎么样？
-
2023-12-15 07:19:55
-
- 决战决胜脱贫攻坚云新明赴我县调研脱贫攻坚、农牧业产业和生态建设工作
-
2023-12-15 07:17:40
-
- 花奇楠类似奇楠沉香？那可大不一样，你上当了吗？
-
2023-12-15 07:15:26
-
- 和腾讯王卡一较高下，电信王卡五系应用全免流，全网免流时代来啦
-
2023-12-15 07:13:11
-
- 风水鱼之龙鱼的讲解
-
2023-12-15 07:10:56
-
- 分享一组《灌篮高手》手机壁纸，满满的回忆喜欢收下吧
-
2023-12-15 07:08:41
-
- 电容的那些公式儿
-
2023-12-15 07:06:26
-
- levante中文名，你知道是什么吗？它旗下有哪些车呢？
-
2023-12-15 07:04:11
-
- KPL解说大全：最美解说天云
-
2023-12-15 07:01:56
-
- 年纪最大的十位开国将帅（组图）
-
2023-12-15 00:18:46
-
- 就凭这一条 燕郊划给北京的可能性为零 你还会买燕郊的房子吗？
-
2023-12-15 00:16:31
-
- 教大家一分钟自测有没有甲亢
-
2023-12-15 00:14:16
雾都朱豪将军原型是谁(雾都中朱豪将军是一个虚构的人物)
星甲魂将传原著小说